Irreducible ideal

In mathematics, an ideal of a commutative ring is said to be irreducible if it cannot be written as a finite intersection of ideals properly containing it.

Every prime ideal is irreducible. Every irreducible ideal of a Noetherian ring is a primary ideal, and consequently for Noetherian rings an irreducible decomposition is a primary decomposition. Every primary ideal of a principal ideal domain is an irreducible ideal. Every irreducible ideal is a primal ideal.

An element of an integral domain is prime if, and only if, an ideal generated by it is a nonzero prime ideal. This is not true for irreducible ideals: an irreducible ideal may be generated by an element that is not an irreducible element, as is the case in 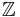$\mathbb Z$ for the ideal 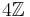$4 \mathbb Z$ : It is not the intersection of two strictly greater ideals.

The notion is more easily understood in terms of algebraic geometry. An ideal I of a ring A is irreducible if, and only if.the algebraic set it defines is irreducible (that is, any open subset is dense) for the Zariski topology, or equivalently if the closed space of spec A consisting of prime ideals containing I is irreducible for the spectral topology.

If k is an algebraically closed field, choosing the radical of an irreducible ideal of a polynomial ring over k is the same thing as choosing an embedding of the affine variety of its Nullstelle in the affine space.